Esta semana, Santiago Olmedo, profesor de Química y Termodinámica de nuestra carrera comparte con nosotros su visión matemática sobre las notas musicales. ¿Se les había ocurrido alguna vez pensar que todo tenía una explicación matemática?
Todos los sonidos son producidos por algunos procesos físicos que tienen un carácter periódico como una cuerda vibrando o el aire en el interior de un instrumento de viento. Aun siendo muy diferentes entre ellos, estos procesos pueden ser descritos con un mismo modelo matemático. La característica más fundamental de esos sonidos es su frecuencia. Imaginémonos una cuerda que al ser tocada vibra, dando oscilaciones en las proximidades de su posición de reposo o equilibrio. Cuantas más oscilaciones da en un período de tiempo, más alta será la frecuencia del sonido producido, y más agudo será el sonido resultante. La magnitud de la frecuencia se mide en Hertz (Hz), que es simplemente el número de oscilaciones o ciclos por segundo. En la música occidental cada sonido o nota musical tiene su frecuencia definida. Todas las melodías son una combinación de varias notas es decir de estas frecuencias en diferentes intervalos de tiempo.
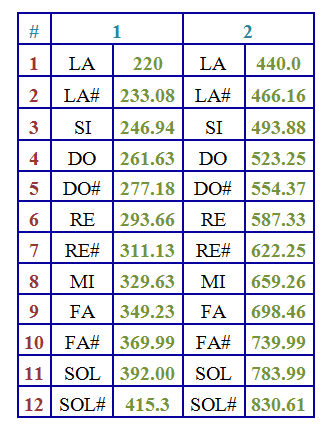
En la escala cromática, entre una nota y su octava, o sea el doble de su frecuencia inicial se encuentran doce sonidos eso quiere decir doce notas intermedias. La nota fundamental es el LA central de un piano que representa 440 Hz. En base de esta frecuencia se pueden encontrar las frecuencias de todas las notas.
Entonces que las notas se comportan como una progresión geométrica decreciente infinita, siendo una progresión geométrica es una sucesión de términos tales que cualquiera de ellos es igual al término anterior multiplicado por un número fijo. Este número fijo, se llama razón de la progresión y se representa por r.
En un instrumento de cuerda la distancia total de cada cuerda se la va a representar por l, y cada traste, o pieza metálica a lo largo del mástil o cuello del instrumento se la va a definir como an. Para conocer el desarrollo matemático de la ecuación hacer clic aquí.
Esta ecuación fue verificada para instrumentos que fueron desde un bajo electro acústico de una longitud cuerda de casi 90 cm hasta mandolinas de 40 cm de longitud. Finalmente para comprobar la eficiencia de la ecuación se construyó un instrumento denominado charango eléctrico que no necesitó de amplificación física (caja de resonancia) porque su amplificación era netamente electrónica por medio de micrófonos de bobina y cuerdas de acero que al vibrar perturbaban el campo eléctrico de la bobina principal. Siendo el resultado el charango presentado:
Santiago Olmedo, MSc.